Warum werden Windräder immer größer?

Diesen Artikel gibt es auch als animiertes Video!

Windräder werden immer größer!

Einer der vielen Konflikte, die um die Windkraft ausgefochten werden, betrifft die Größe der Anlagen. Manche Bürgerinitiative fordert: Windkraft ja, aber bitte kleinere Anlagen! Auch die 10H-Regel in Bayern versucht, die Anlagen möglichst klein zu halten. Und tatsächlich werden die Windkraftanlagen immer größer. Folgende Grafik zeigt das eindrucksvoll.

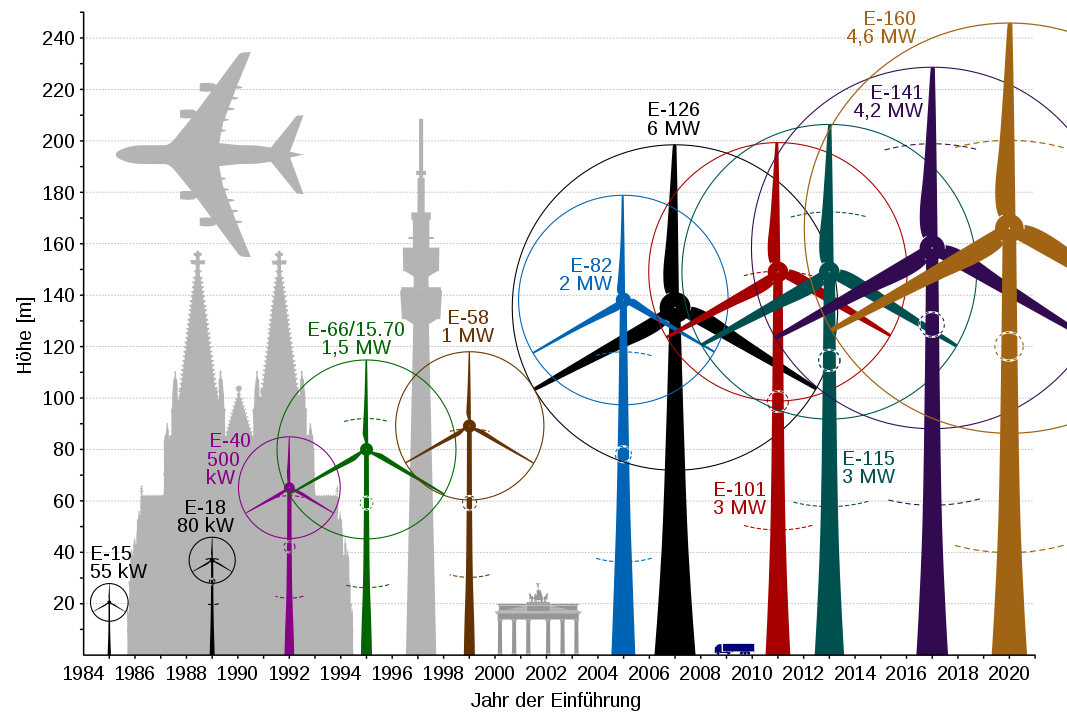
Auch die Datenbank wind-turbine-models bestätigt diese Entwicklung

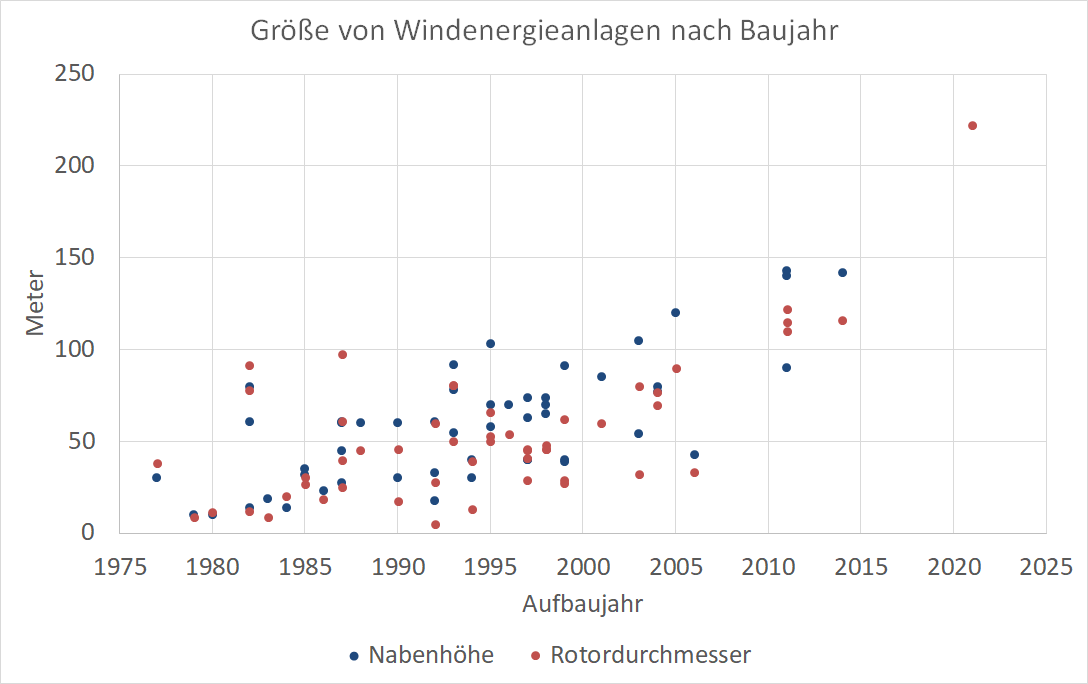
Aber warum ist das überhaupt so? Was bringt es, Windräder immer größer zu bauen? Und wie viel Energie steckt eigentlich überhaupt im Wind?

Wie viel Energie steckt eigentlich im Wind?

Um das zu berechnen, beginnen wir mit der Grundformel für die Bewegungsenergie, also die Arbeit, welche nötig ist, um irgendetwas vom Stillstand auf eine bestimmte Geschwindigkeit v zu beschleunigen – oder umgekehrt, die Energie, welche frei wird, wenn dieser Gegenstand abgebremst wird. Klar ist, dass diese Energie davon abhängt, wie schwer das Objekt ist (also wie groß seine Masse m ist) und wie schnell es am Schluss sein soll (oder vor dem Abbremsen war). Aber wie genau? Eine der besten Dinge an der Physik ist, wenn man sich ein paar Formel zusammensucht, sie ineinander einsetzt und daraus etwas neues berechnet. Und das machen wir jetzt.

Um das Objekt in Bewegung zu setzen, zu beschleunigen, müssen wir eine Kraft F auf das Objekt ausüben. Und wer in der Schule Physik hatte, der weiß noch, Arbeit = Kraft mal Weg. Das ist unsere Formel Nummer eins:

Formel Nummer zwei aus dem Physikunterricht: Kraft = Masse mal Beschleunigung:

So, jetzt basteln wir die zwei zusammen und bekommen:

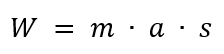
In dieser Formel steckt bereits die Geschwindigkeit. Um das zu sehen, schauen wir uns zuerst mal den Weg s in unserer Formel an. Der hängt nämlich folgendermaßen von der Beschleunigung a und der Zeit t ab (noch eine Formel aus dem Physikunterricht):

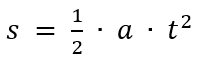
Und wenn wir jetzt diese zwei zusammenfügen, dann bekommen wir:

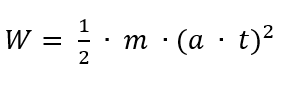
Sieht noch nicht so aus, als wären wir unserem Ziel, die Geschwindigkeit in der Formel zu haben, irgendwie näher gekommen. Aber es fehlt nur noch ein Schritt, und dazu brauchen wir Formel Nummer vier aus dem Physikunterricht: Beschleunigung ist Geschwindigkeit pro Zeiteinheit:

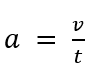
Und wenn wir diese zwei zusammenfügen, sind wir am Ziel:

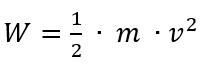
Bis hierher ist die Formel allgemeingültig für jedes bewegte Objekt. Wenn wir sie für Windenergie anwenden wollen, müssen wir herausfinden, wie groß die Masse in unserer Formel ist, denn klar, v ist die Windgeschwindigkeit. Die Masse, deren Bewegungsenergie wir ernten wollen, ist natürlich die des Windes, der auf unser Windrad trifft. Wie groß ist die? Ganz allgemein und auch für den Wind gilt zunächst mal: Masse ist gleich Dichte mal Volumen.

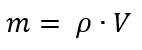
Die Dichte ist hier logischerweise die Dichte der Luft, aber was ist das Volumen? Schauen wir uns mal das Bild eines Windrades an.

Ein Stück vom Wind, dessen Energie wir ernten wollen, ist ein liegender Zylinder, dessen Volumen die von den Flügeln überstrichene Fläche A mal der Tiefe s beträgt (und ja, das ist derselbe Weg s wie gerade eben).

Dieser Zylinder bewegt sich durch unser Windrad hindurch, und zwar mit der Geschwindigkeit v. Dafür braucht er die Zeit t.

So, ihr kennt das Spiel inzwischen, das setzen wir jetzt beides in unsere Formel für die Masse ein und erhalten:

Letzter Schritt, die Formel für m eingesetzt in die Formel für W gibt

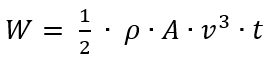
Und das ist jetzt endlich die Energie, die wir dem Wind während der Zeit t entnehmen können. Wenn wir wissen wollen, wie viel unser Windrad leistet, dann lassen wir die Zeit einfach weg, denn die Leistung P ist Arbeit W pro Zeit t

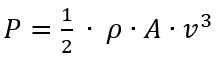
Diese Formel ist die Standard-Industrieformel um zu berechnen, wie viel Leistung eine Windenergieanlage überhaupt haben kann. Natürlich kann man nicht die gesamte Energie entnehmen (dazu kommen wir noch), aber es ist die physikalische Obergrenze. Mehr Energie ist einfach nicht drin! So, aber wir haben das ja nicht nur zum Spaß berechnet, sondern wir wollen ja auch was lernen. Und in der Tat können wir an dieser Formel zwei interessante Dinge ablesen:

Windgeschwindigkeit

Zum einen hängt die Leistung in der dritten Potenz von der Windgeschwindigkeit ab. Wenn also der Wind doppelt so schnell weht, dann ist der Ertrag nicht doppelt, sondern acht Mal so groß! Völlig klar also, dass man dahin muss, wo der Wind schneller weht – und das schauen wir uns mal genauer an.

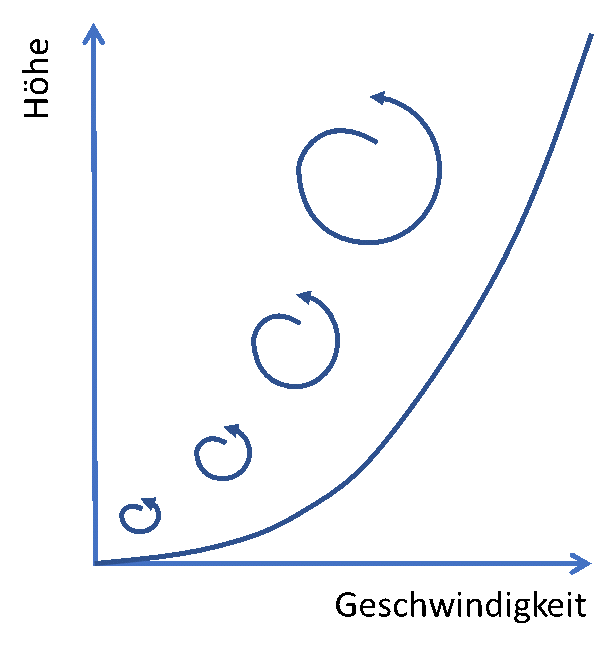
Wenn eine Flüssigkeit (und in der Physik gilt auch die Luft als Flüssigkeit) an einem festen Körper entlangströmt, wird sie abgebremst. Der Ingenieur Ludwig Prandtl stellte 1904 fest, dass sich das Verhalten eines solchen Fluids in zwei Bereiche einteilen lässt: Eine Außenströmung, in der keine Hindernisse im Weg sind und die Flüssigkeit frei und gleichmäßig strömt – eine laminare Strömung. Und eine Grenzschicht, in der die Reibung des Hindernisses wirkt und Turbulenzen verursacht, die die Strömung bremsen. Direkt am Körper ist die Geschwindigkeit gleich Null, die Teilchen bleiben haften. Je weiter wir vom Körper weggehen, desto schneller bewegen sie sich. Wenn wir 99% der Umgebungsgeschwindigkeit erreicht haben, haben wir die Grenzschicht verlassen.

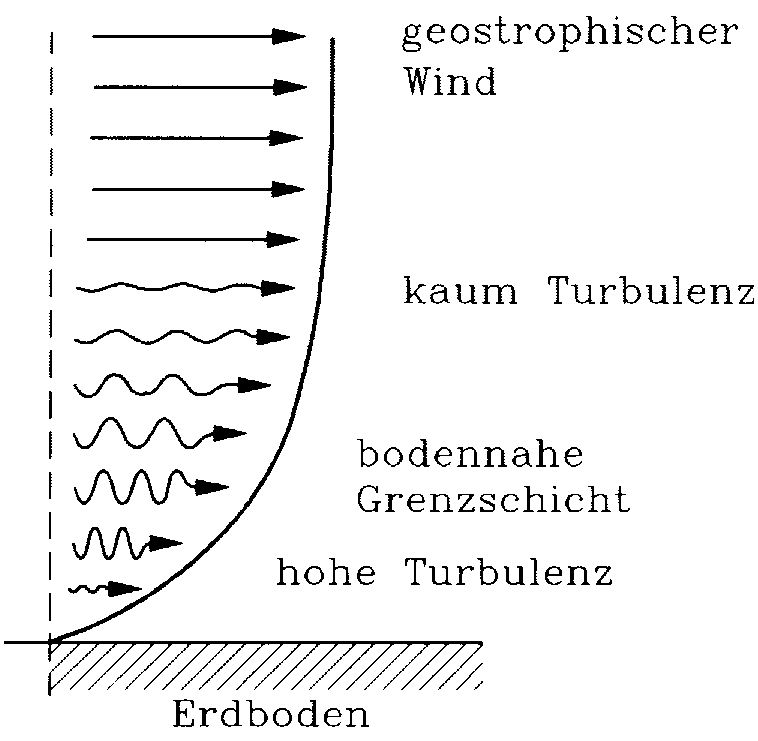
Die spannende Frage ist nun, wie dick ist diese Grenzschicht und wie ist das Geschwindigkeitsprofil innerhalb der Schicht?

Turbulenzen sind im Grunde nichts anderes als Spiralen, die quer zur Hauptfließrichtung liegen und dafür sorgen, dass sich die Flüssigkeit durchmischt.

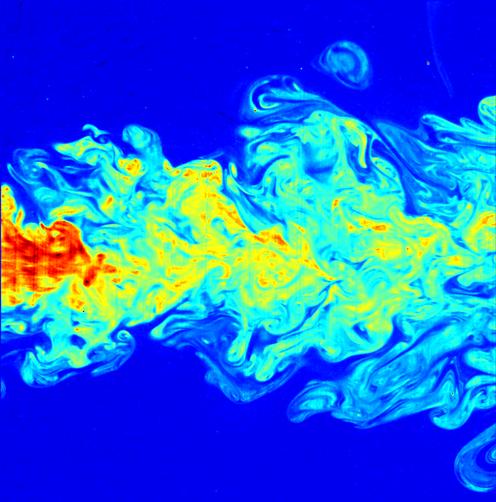
Prandtl stellte fest, dass die Turbulenzen umso größer sind, je weiter sie vom Hindernis entfernt sind.

Daraus leitete er folgende Formel ab:

Die Geschwindigkeit v in der Höhe h ist gleich der sogenannten Schubspannungsgeschwindigkeit v* geteilt durch die von-Karman-Konstante κ, multipliziert mit dem natürlichen Logarithmus des Verhältnisses der Höhe zur sogenannten Rauigkeitslänge h₀. Puh! Eine Menge neuer Begriffe, und insbesondere die Schubspannungsgeschwindigkeit und von-Karman-Konstante sind in der Praxis schwer zu bestimmen, deswegen behilft man sich mit einem mathematischen Trick. Wenn man nämlich durch Messungen die Windgeschwindigkeit v_r in einer bestimmten Höhe h_r kennt (der Index r steht für Referenz), dann kürzen sich v* und κ heraus, und man kann die Geschwindigkeit in einer anderen Höhe h folgendermaßen bestimmen:

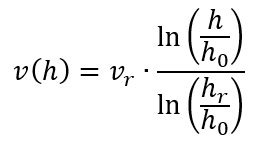
Aus dieser Gleichung, so kompliziert sie aussieht, lernen wir zwei Dinge. Erstens, dass die Windgeschwindigkeit mit dem Logarithmus der Höhe zunimmt – also umso schneller je tiefer wir noch sind und immer langsamer, je höher wir schon sind.

Und zweitens, dass die Krümmung dieser logarithmischen Kurve, d.h. auf welcher Höhe wir die laminare Strömung erreichen (die Dicke der Grenzschicht also) von der Rauigkeitslänge h₀ abhängt. Und das ist trotz des seltsamen Namens eine einleuchtende Größe: Nämlich die Höhe über dem Erdboden, bei der die Windgeschwindigkeit noch Null ist. Und natürlich hängt das davon ab, wie viele Hindernisse da im Weg herumstehen. So ist die Rauigkeitslänge über einer glatten Wasseroberfläche ein zehntel Millimeter, bei bewegter See drei Millimeter, über Äckern drei Zentimeter, über einem Wald achtzig Zentimeter und in der Stadt ein Meter. Klingt nach wenig, aber man muss sich zum einen klar machen, dass darunter im Mittel komplette Windstille herrscht (egal wie sehr es oben bläst) und zum anderen wie groß die Unterschiede sind – vier Größenordnungen! Dementsprechend unterscheidet sich die Windscherung je nach Bodenbeschaffenheit enorm.

Und das ist der wahre Grund, warum Windräder nicht in der Stadt gebaut werden – dort muss man viel höher hinaus. Nicht wegen des angeblichen Infraschalls. Hinzu kommt: Über Land können die einzelnen Hindernisse so eng zusammenstehen, dass die Oberkante dieser Hindernisse wie eine neue Oberfläche wirkt, oberhalb derer erst die Rauigkeitslänge beginnt. Dies gilt insbesondere über Wald und dichter Bebauung.

Exkurs: Es ist noch viel komplizierter

Im Detail ist es natürlich alles noch komplizierter, so ist zwischen der Prandtl-Schicht, in der obige Formel gilt und der laminaren Außenströmung noch eine weitere Schicht, die sogenannte Ekman-Schicht.

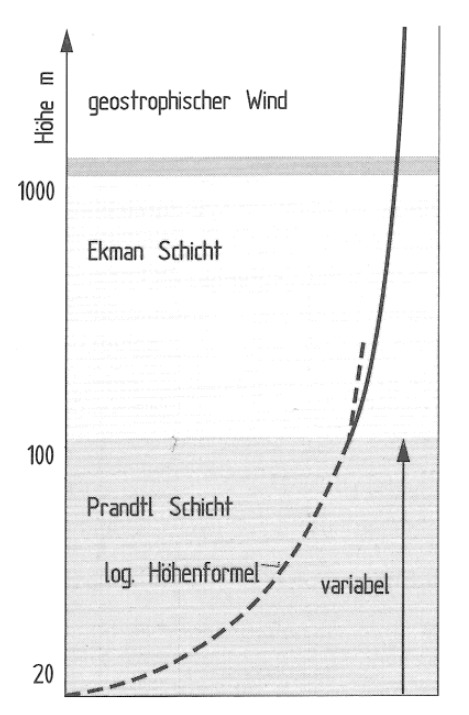
Und in der Ekman-Schicht dreht sich die Windrichtung aufgrund der Coriolis-Kraft zu allem Unglück auch noch um 90°.

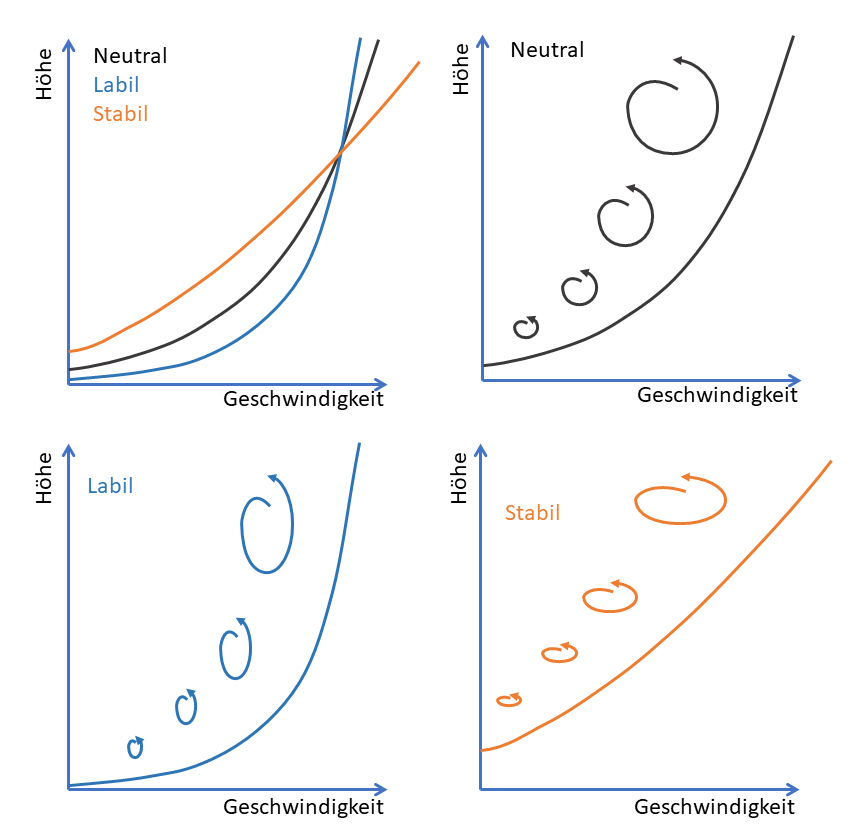
Und drittens gilt das schöne logarithmische Profil nur dann, wenn die Atmosphäre „neutral“ ist – also die Turbulenzen ungefähr kreisförmig sind. Wenn die Temperaturunterschiede zwischen oben und unten anders sind („labil“ oder „stabil“), und dadurch die Turbulenzen steiler oder flacher sind, dann verändert sich auch das Profil und wird steiler oder flacher.

Windräder im Wald

So, aber warum werden dann Windräder über Wald gebaut? Das ist ja noch so ein Kritikpunkt vieler Bürgerinitiativen und Politiker gegen Windkraft – „das lohnt sich nicht!“ Ha, und jetzt haben wir ja sogar Formeln, um zu beweisen, dass sich das nicht lohnt! Also basteln wir unsere zwei Formeln (die Industrieformel zur Leistung und die Prandtlsche Höhenformel) mal zusammen und setzen Zahlen ein. Wir nehmen zwei Windräder mit gleicher Fläche (A=2000 m²) und bauen eines aufs flache Land (Rauigkeitslänge h₀ = 0,03m) und eines in den Wald (h₀ = 0,8m). Bei beiden gehen wir von einer Referenzgeschwindigkeit v_r = 5 m/s in einer Höhe h_r von 80 m über Grund aus (das ist die mittlere Windgeschwindigkeit in den meisten Gegenden in Deutschland) und einer Luftdichte von ρ = 1,225 kg pro m³. Wie hoch muss jeweils der Mast sein, damit wir eine Leistung von P = 0,2 MW erzielen?  Ich erspare uns die Umformungen und Einsetzungen (wie steht in den Mathebüchern immer so schön, wenn der Autor zu faul ist? „Wie der geneigte Leser leicht erkennt“), aber die resultierende Formel ist:

Jetzt setzen wir unsere Zahlen ein und erhalten ein völlig verwirrendes Ergebnis: Über dem Acker müssen wir 167m hoch bauen, über dem Wald aber nur 123m.

Wait, WHAT? Das ist doch falsch rum! Da muss ein Fehler drin sein!

Tatsächlich, aber kein Fehler in der Mathematik, sondern ein Denkfehler: Wenn nämlich auf derselben Höhe über dem rauen Wald der Wind genauso stark bläst wie über dem glatten Ackerland, dann muss er weit oben im laminaren Bereich über dem Wald viel stärker sein als über dem Acker. Klar soweit?

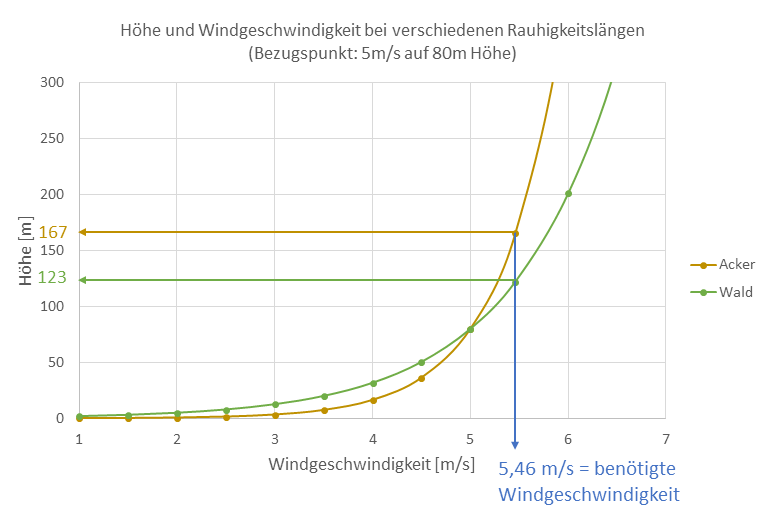
Daraus könnten wir jetzt folgendes schließen: Über dem Wald kann der Wind unmöglich so schnell sein wie über dem Acker, d.h. unsere Annahme gleicher Windgeschwindigkeit auf 80m Höhe ist in der Praxis falsch. Allerdings, wenn wir uns den Windatlas für Deutschland mal anschauen, dann finden wir über den meist bewaldeten Mittelgebirgen ähnliche Farben wie in der Norddeutschen Tiefebene.

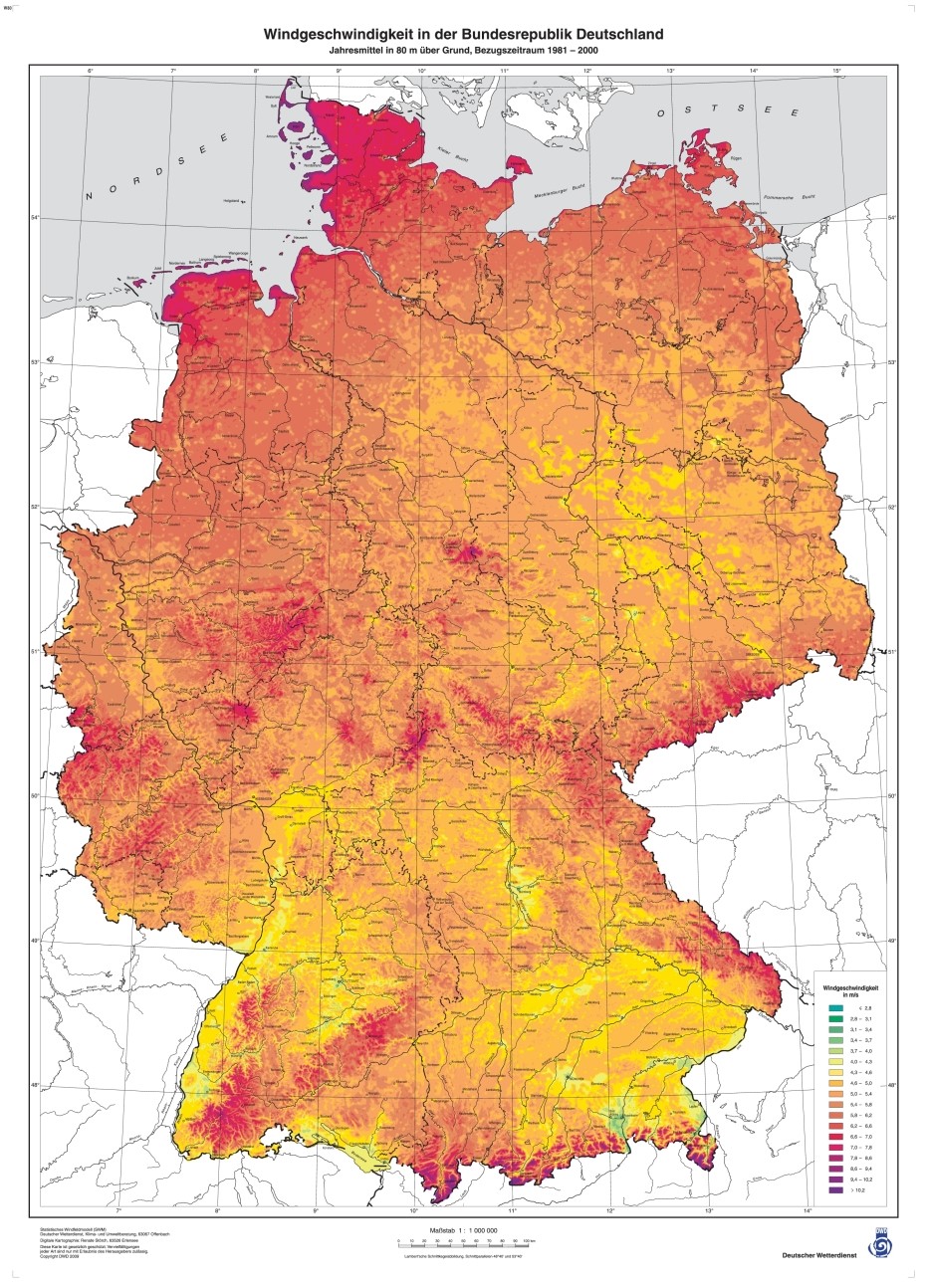
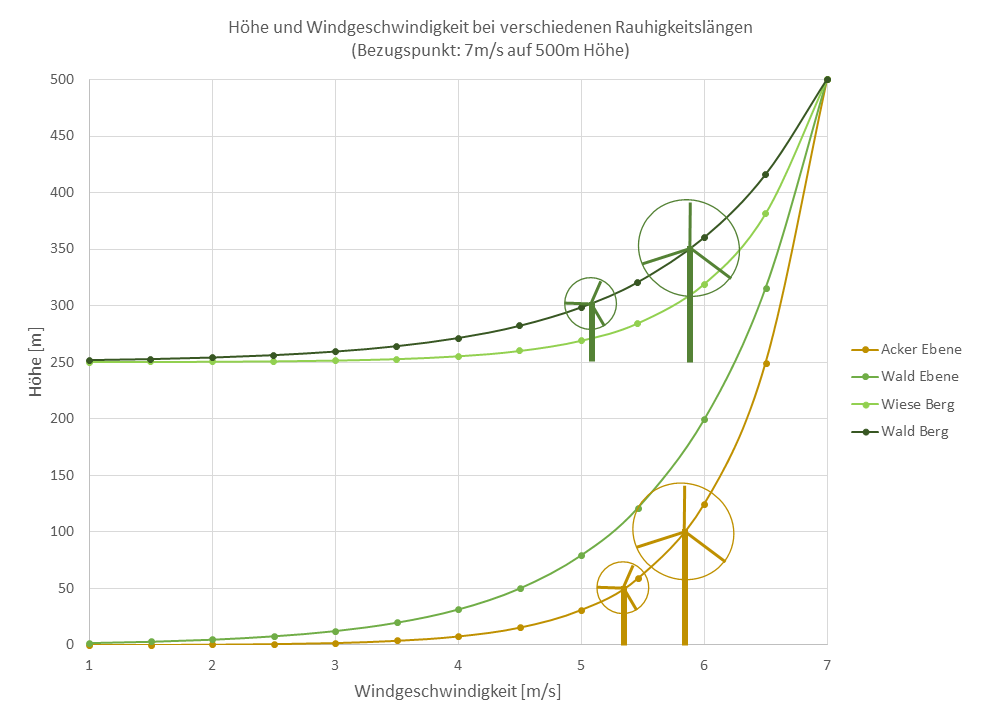
Und das bedeutet: Diese Gebirgslagen sind außerordentlich ertragsreich – der Wind bläst dort trotz all der Bäume ringsum genauso stark wie am Meer – jeder Meter höher bringt also überproportional mehr Ertrag! Folgende Grafik veranschaulicht es auf andere Weise: Angenommen der laminare Bereich beginnt bei 500 m und dort weht der Wind mit einer Geschwindigkeit von 7 m/s. Ein 50m hohes Windrad erreicht auf einem Acker in der Ebene eine Windgeschwindkeit von ca. 5,4 m/s, stellt man dasselbe Windrad auf einem bewaldeten Berg von 250m Höhe, so erreicht es nur 5,1 m/s. Baut man das Windrad aber 100m hoch, so erreicht es auf dem Acker in der Ebene 5,8 m/s, auf dem bewaldeten Berg aber 5,9 m/s!

---

---

Rotorfläche

Jetzt wenden wir uns endlich der zweiten Variable in unserer Industrie-Leistungsformel zu, der Fläche A. Die ist bei den üblichen Anlagen ein Kreis mit dem Radius r:

Und r ist hierbei natürlich die Flügellänge. Das heißt, dass die Leistung mit dem Quadrat der Flügellänge steigt. Doppelt so lange Flügel bringen den vierfachen Ertrag. Und das ist natürlich der Grund dafür, dass die Flügel immer länger werden.

Aber noch etwas ist wichtig an unserer Formel. Wenn wir Industrie-Leistungsformel durch die Fläche teilen, und die Leistung pro Quadratmeter (d.h. die Energieflussdichte ψ) berechnen, erhalten wir

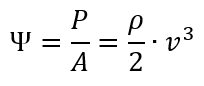
In diese Formel können wir mal spaßeshalber die typische Windgeschwindigkeit für 10 Meter Höhe einsetzen, in der üblicherweise Kleinwindanlagen stehen, nämlich 3 m/s (fast überall in Deutschland außer in der norddeutschen Tiefebene). Dann erhalten wir eine maximale Energieflussdichte von 16,54 Watt pro Quadratmeter. Das bedeutet, dass wir, um ein Kilowatt zu erzeugen, eine Anlage mit mindestens 60 Quadratmeter Fläche brauchen – das sind ca. 4,4m Flügellänge oder ein Quadrat von knapp 8 x 8 Meter.

Wahrer Ertrag

Das ist aber noch nicht das Ende der Geschichte. Denn keine Anlage der Welt kann die gesamte kinetische Energie des Windes ernten – sie müsste ihn dafür zum Stillstand bringen. Eine undurchdringliche Wand würde das tun, aber die erntet wiederum keine Energie. Ein Teil der Energie bleibt im Wind erhalten, der die Anlage hinten wieder verlässt. Spannend ist nun, wie viel das ist und ob es ein Optimum gibt. Mit einigen vereinfachenden Annahmen (das Windrad hat keine Dicke, sie entnimmt die Energie ohne Verluste und die Luft wird nicht komprimiert) hat der Physiker Albert Betz diese Frage bereits 1919 beantwortet.

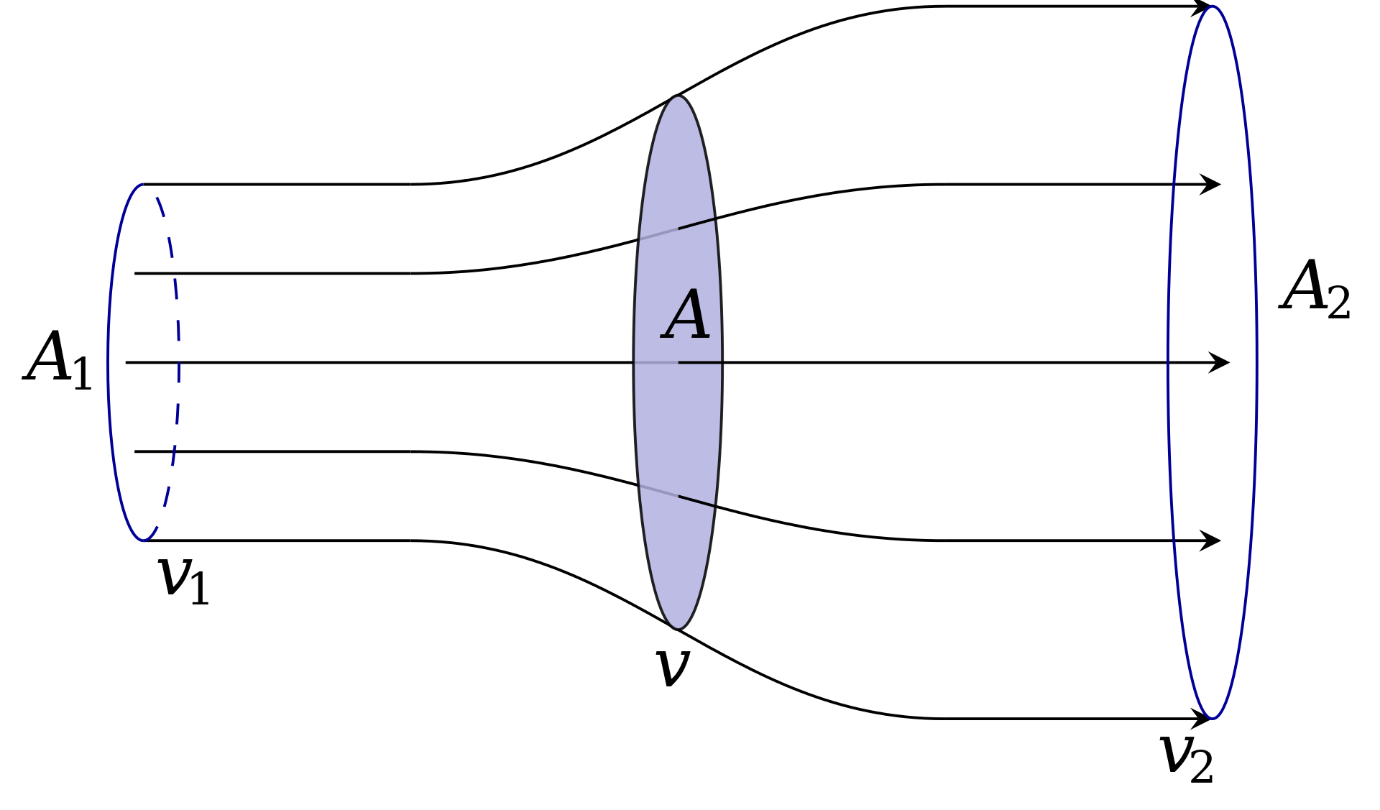
Der Wind, der die Fläche A des Rotors mit der Geschwindigkeit v durchströmt, hat vor dem Auftreffen auf den Rotor die (höhere) Geschwindigkeit v₁ und nimmt die Fläche A₁ ein. Weit hinter dem Rotor hat sie die (langsamere) Geschwindigkeit v₂ und nimmt die größere Fläche A₂ ein. Die Fläche ist deswegen größer, weil ja die ganze Luft, die vorne in das System eingeströmt ist, es hinten auch wieder verlassen muss – und wenn sie dabei langsamer ist, braucht sie mehr Platz, um dieselbe Menge zu transportieren.

Jetzt erinnern wir uns an unsere Herleitung der zentralen Leistungsformel, und zwar dass die Geschwindigkeit, die wir in der dritten Potenz in der Formel haben, eigentlich aus zwei verschiedenen Teilen besteht: Nämlich der Geschwindigkeit, die das Volumen der Luft berechnet, die am Rotor vorbei strömt und der Geschwindigkeit, die wir in Energie umwandeln. Wenn wir das wieder trennen, sieht unsere Formel so aus:

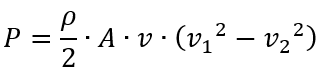
Die Geschwindigkeit v am Rotor wiederum ist der Mittelwert zwischen Anfangs- und Endgeschwindigkeit

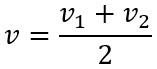
Eingesetzt erhalten wir

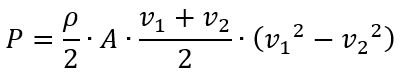
Als nächstes definieren wir die Endgeschwindigkeit v₂ als das x-fache der ankommenden Geschwindigkeit v₁; und da die Endgeschwindigkeit immer kleiner ist als die Anfangsgeschwindigkeit, ist x immer kleiner als 1.

Wenn wir das einsetzen, erhalten wir

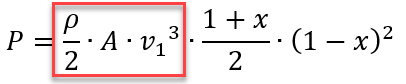
Und der erste Teil dieser Gleichung ist ja die Energie, die unsere Anlage anströmt. Somit ist der zweite Teil

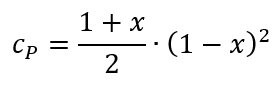
der sogenannte Leistungsbeiwert c_P. Und diese Funktion hat einen sehr interessanten Verlauf.

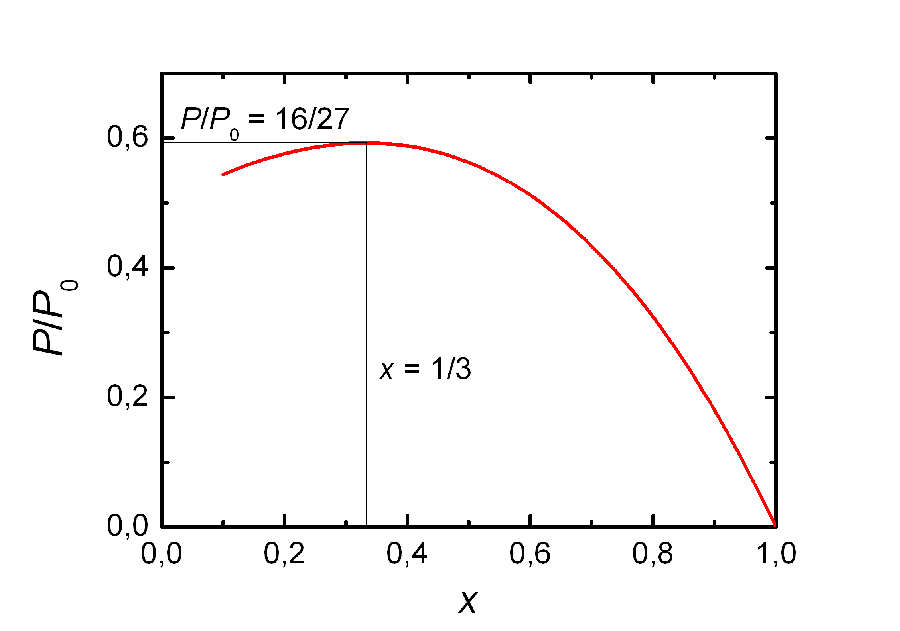
Ein Wert x = 0 bedeutet, dass die Luft vollständig abgebremst wird, v₂ = 0. Aber da die Luft ja irgendwohin muss, wäre die Fläche A₂ unendlich groß, was unmöglich ist. Deswegen beginnt die Kurve real bei 0,1. Ein Wert x = 1 wiederum bedeutet, dass Anfangs- und Endgeschwindigkeit gleich groß sind, das wäre bei einer stillstehenden Anlage der Fall, und deswegen entnehmen wir dann auch keine Energie. Durch Ableiten der Funktion (wer erinnert sich noch an die Kurvendiskussionen in der Oberstufe?) stellt man fest, dass das Optimum bei x = 1/3 liegt. Und der Wert für c_P liegt dann bei 16/27, das ist ca. 0,5926. Das bedeutet, dass man durch eine Turbine dem anströmendem Medium maximal knapp 60% seiner Energie entnehmen kann. Reale Windenergieanlagen mit waagrechter Achse haben einen Leistungsbeiwert von 40%-50%; Rotoren mit senkrechter Achse noch weniger.

Wenn wir das nun in unsere Kleinwindanlage von eben einsetzen, so sehen wir, dass wir für eine Leistung von einem Kilowatt mindestens Flügel von 5,66m Länge benötigen, oder ein Quadrat von 10m Seitenlänge. Und das ist mehr als auf ein gewöhnliches Haus passt, und das ist der Grund dafür, dass sich Kleinwindanlagen selten lohnen – nämlich nur, wenn sie in Gegenden mit wirklich hohen Windgeschwindigkeiten stehen oder eben gar keine so kleinen Anlagen mehr sind.

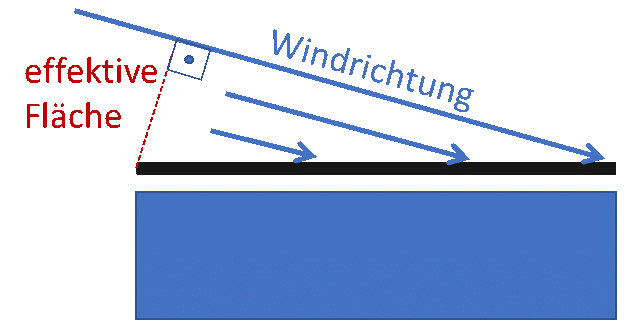
Und mit diesem Wissen können Sie jetzt auch direkt sehen, warum Wunder-Anlagen wie Windwände oder ähnliches in aller Regel Fake sind. Bei diesen kommt übrigens noch etwas hinzu: Wenn die Windwände vor einer normalen Wand montiert sind, kann die Luft auf der Rückseite nicht entweichen – es entsteht ein Windstau und der Ertrag ist null. Falls die Windwand dagegen seitlich angeströmt wird, ist wiederum die effektive Fläche sehr viel kleiner – wie groß, das kann man mit dem Pythagoras ausrechnen.

Materialbedarf

Jaja, werden manche jetzt sagen, aber größere Anlagen brauchen ja auch mehr Material! Und wenn man den Ertrag pro Ressourceneinsatz betrachtet, dann ist es bestimmt egal, ob man viele kleine oder wenige große Anlagen aufstellt! Nun, das ist ein guter Einwand, und dem wollen wir nachgehen. Wir brauchen also zwei Formeln, zum einen die Leistung abhängig von der Größe der Anlage und zum anderen den Materialbedarf abhängig von der Größe. Der Einfachheit halber machen wir ein paar Annahmen:

1. Wir skalieren die Anlage maßstabsgetreu. Wir machen sie also nicht schlanker oder fragiler und wir verzichten auch auf besondere verstärkende Elemente.
2. Wir setzen den Materialbedarf mit dem Volumen gleich
3. Wir betrachten nur die Verhältnisse des Materialbedarfs abhängig von der Größe – das erlaubt uns nämlich, die Form der Anlage radikal zu vereinfachen.
   

Mit diesen Annahmen konzentrieren wir uns auf dem Mast und denken ihn uns als schlanken Hohlzylinder mit der Höhe h, dem Innendurchmesser d_i und dem Außendurchmesser d_a. Alle drei Größen skalieren wir mit dem Faktor x. Das Volumen des Mastes beträgt:

wobei G(x) die Grundfläche ist und sich folgendermaßen berechnet:

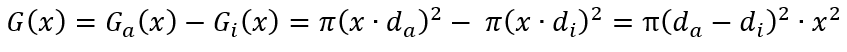
Wenn wir das einsetzen, erhalten wir

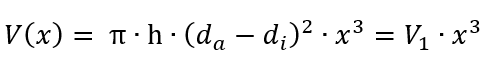
Das benötigte Material steigt also kubisch mit der Größe der Anlage. Nun ja, das hätten wir uns ja denken können – immerhin ist das Volumen die dritte Dimension! Damit können wir uns weitere Rechnerei sparen und wissen, egal wie die Anlage konkret aussieht, doppelte Größe benötigt achtfaches Material.

Als nächstes schauen wir uns die Leistung an. Für die bringen wir unsere allgemeine Leistungsformel, die Prandtlsche Höhenformel und die Formel für die Rotorfläche zusammen:

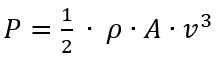
Dazu betrachten wir ein Windrad der Referenzhöhe h_r, welches wir mit dem Faktor x skalieren. Für den Radius r der Rotorfläche, also die Flügellänge, nehmen wir das f-fache der Masthöhe (also f mal h_r, wobei f < 1); dann sehen unsere drei Formeln so aus:

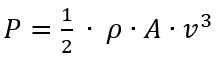
Wenn wir das jetzt ineinander einsetzen, erhalten wir

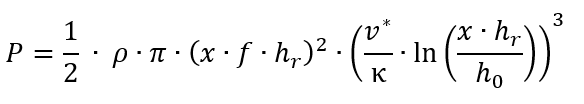
Das können wir noch vereinfachen und zusammenfassen

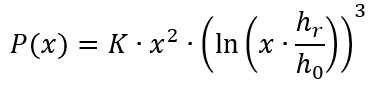
Im letzten Schritt haben wir alle Konstanten zu einer Mega-Konstante K zusammengefasst. Das Verhältnis Referenzhöhe zur Rauigkeitslänge h_r/h₀ bekommen wir interessanterweise aber nicht weg. Jetzt können wir die Konstanten V₁ und K so wählen, dass eine Anlage der Größe x = 1 ein Volumen von 1 hat und eine Leistung von 1 – und dann ausrechnen, das wievielfache an Volumen und Leistung eine identische, aber x-fach so große Anlage hat. Und folgendes kommt heraus:

Eine doppelt so große Anlage braucht das achtfache an Material und liefert über Wald das sechsfache, über Ackerland das fünffache an Energie. Warum baut man dann nicht einfach mehr kleine Anlagen, wenn das Verhältnis so schlecht ist? Na ja, wenn man vier Anlagen hat und durch zwei doppelt so große ersetzt, braucht man zwar 16 Einheiten Material, aber man bekommt 10 Einheiten an Energie – bei gleichem oder sogar geringeren Platzbedarf. Um dieselbe Menge Energie mit den kleineren Windrädern zu bekommen, bräuchte man zehn Stück davon – die benötigen zwar nur 10 Einheiten Material, aber eben auch 10 Einheiten Platz.

Und der Materialbedarf kann durch gute Ingenieurtechnik gesenkt werden – der Platzbedarf nicht. Wie sieht es denn in der Realität aus? Die folgende Grafik zeigt 449 unterschiedliche reale Windenergieanlagen – ihr Gesamtgewicht aufgetragen über der Nabenhöhe, dazu unsere Schätzung für das Gewicht (skaliert auf den Median aller 50m hohen Windräder). Und es fällt auf, dass die größeren Windräder tendenziell leichter sind als unsere Schätzung!

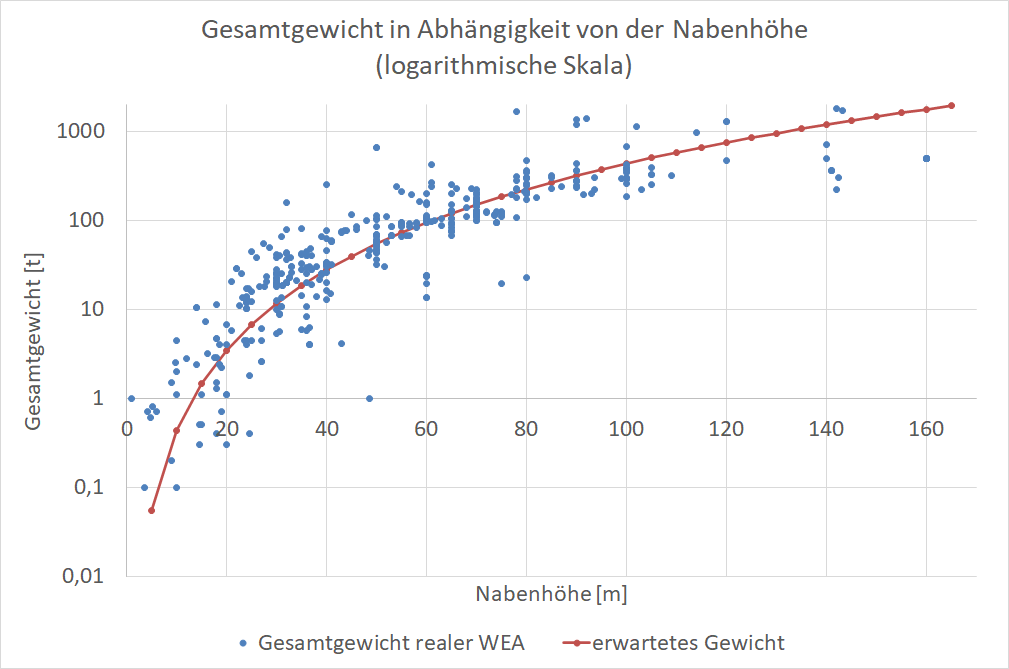
Die nächste Grafik zeigt dieselben Windräder, diesmal die Nennleistung aufgetragen über der Nabenhöhe, dazu unsere Schätzung (skaliert auf den Mittelwert aller 30m hohen Windräder). Auch hier passt die Schätzung faszinierend gut.

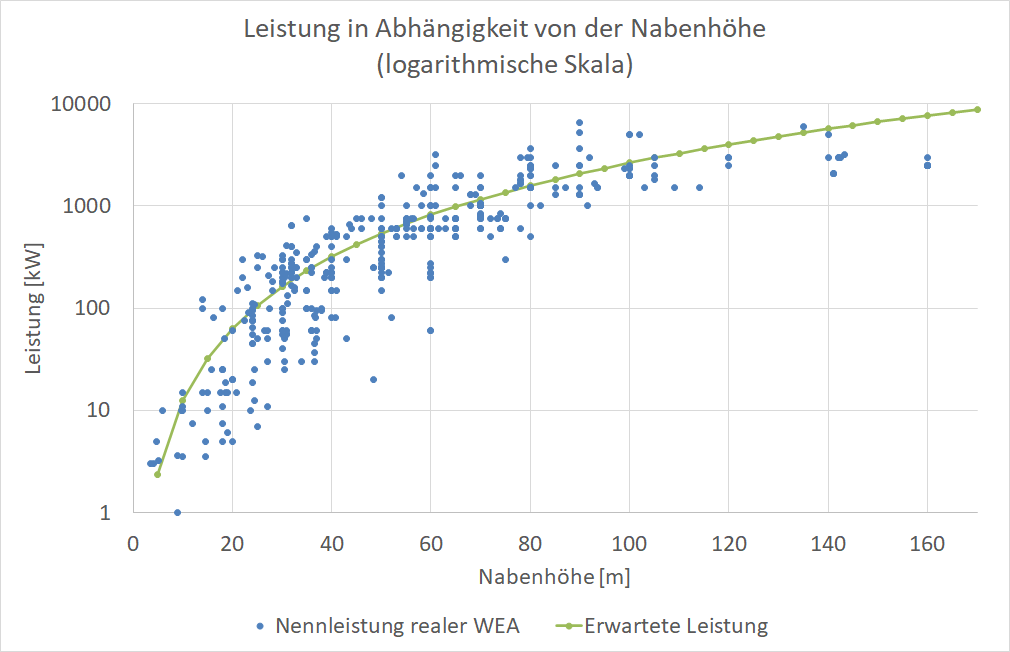
Aber angesichts der Schwankungen um unsere Schätzung wird klar: Ganz offensichtlich ist die Ingenieurleistung wesentlich für beide Größen. Und es ist faszinierend zu sehen, wie viel mehr Energie mittlerweile von einem Windrad gewonnen werden kann – das aktuell leistungsstärkste und größte Windrad der Welt hat einen Rotor von 222 Metern Durchmesser und eine Nennleistung von 14 Megawatt!

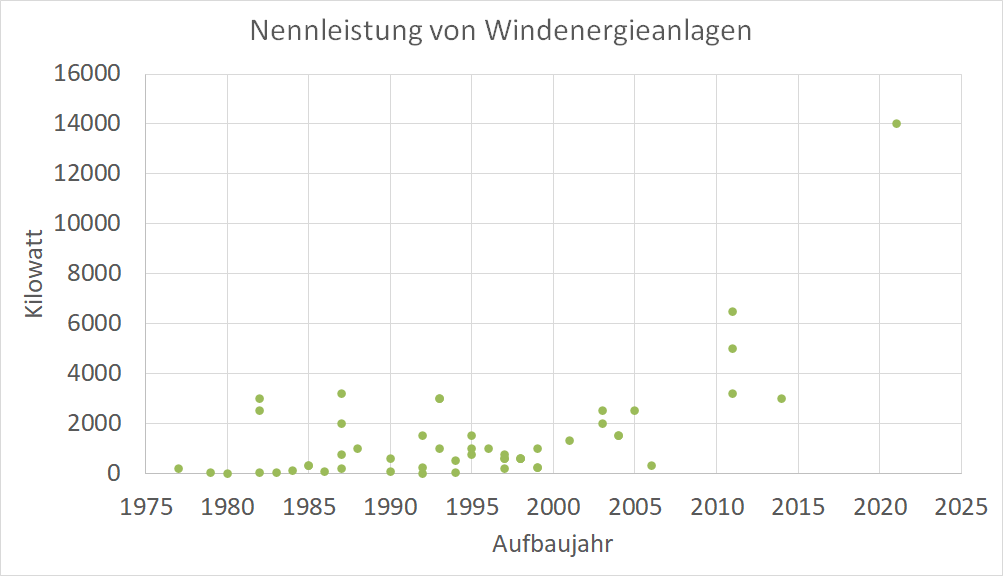
Und während die Windräder in den letzten Jahrzehnten immer größer wurden, und daher die reine Menge an Material pro Windrad anstieg, ist etwas Faszinierendes passiert:

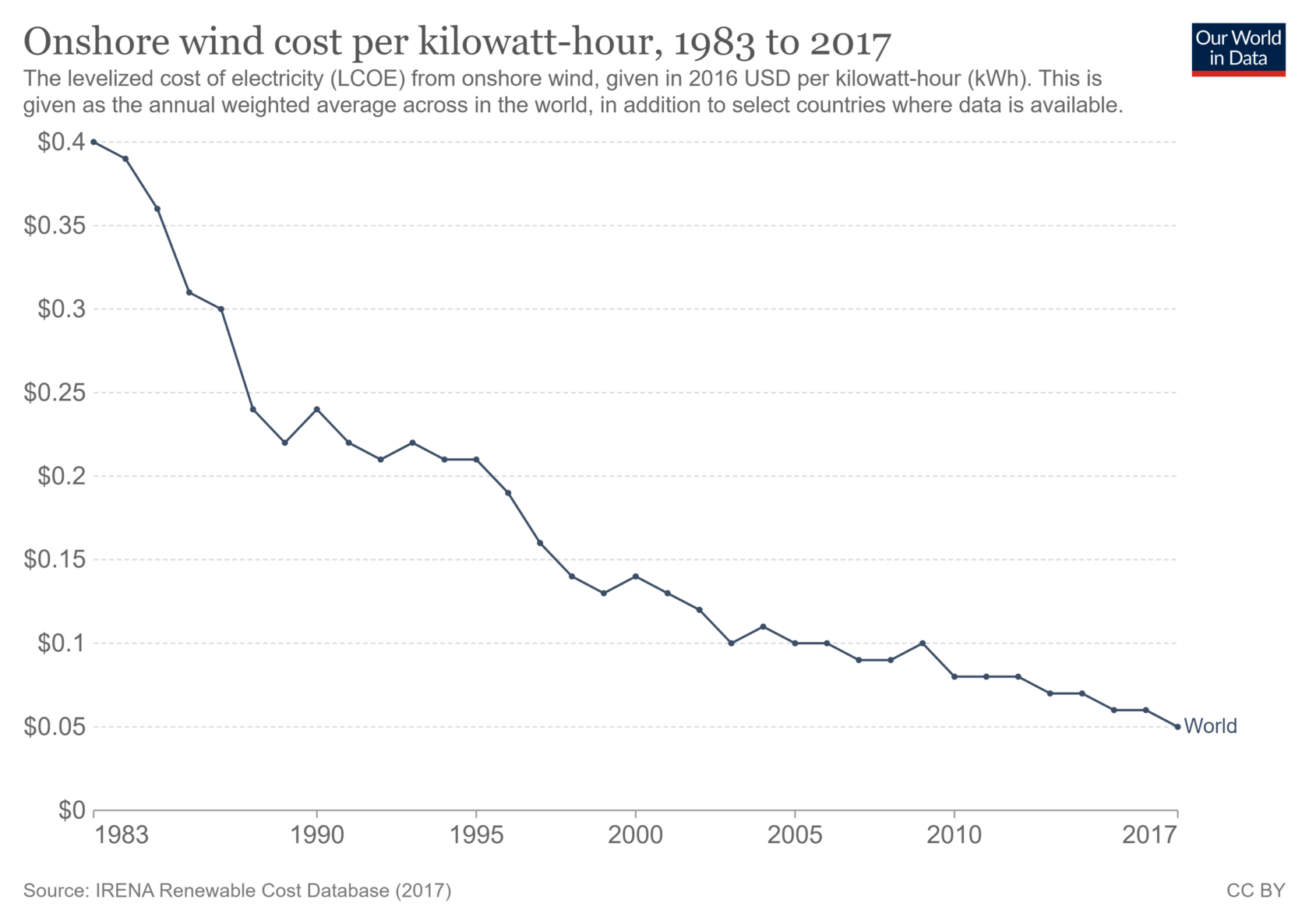
Die Kosten pro Kilowattstunde sind massiv gefallen! Die Materialkosten sind also überhaupt nicht das Entscheidende, sondern die Genialität der Ingenieure. Wenn ihr mehr darüber wissen wollt, was dieser Preisverfall für Auswirkungen hat, empfehle ich euch diesen Artikel.

Also nochmal zusammengefasst – es wird immer billiger, große Windräder zu bauen, gleichzeitig liefern sie ein Vielfaches an Energie (und dank unserer Formeln wissen wir jetzt auch wie viel mehr und warum) und brauchen viel weniger Platz.